Investigating the ELO system (design)

Introduction

Practically every modern, competitive, multiplayer game has a system of matchmaking. Matchmaking is a general term for the behind-the-scenes algorithms that execute when a player clicks "play". The game has an index of how skilled it thinks each player is, and tries to match similarly-skilled players up against each other. Then, after the game has concluded, it updates the index based on the result of the match to better reflect the actual skill of the players.

As someone who almost solely plays multiplayer games, I wanted to learn more about how this system worked. So this week I wrote up some code in the Unity game engine to preform some simulations. My hope was that by implementing a faux matchmaking system myself, I would have a better understanding of the system as a whole.

History

Before modern matchmaking systems, most video games had a setup using a server browser. Instead of entering a matchmaking queue (where you wait for the game to place you in a match), you were able to see a list of all the available games.

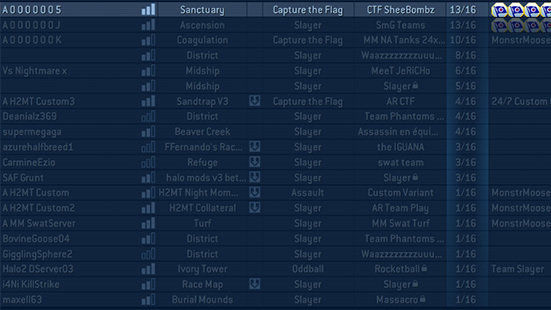
An example of a server browser. The game type, player count, and other information could help you choose which server you wanted to join

Early games chose this approach for a couple reasons. First, there just wasn't enough players to implement a skill-based matchmaking system. If you had to wait for 7 other players of similar skill to join - you could be waiting for hours before your game started.

Secondly, it allowed you to easily play with your friends. You both could simply boot up the game, search for the same server, and play. There wasn't any "hoping" that the game would put both friends in the same lobby.

This system worked well enough. But as games developed and multiplayer grew to be more competitive, it was clear it had some major problems.

• The complete lack of skill-tracking meant a very experienced player could jump in a game with a bunch of new players and slaughter them all. This wasn't fun for either party.

• You weren't rewarded for doing well. The system wasn't tracking your wins and losses, so once you logged off, all of your progress was gone. This didn't incentivize coming back or trying to improve.

• These servers were often hosted by the players themselves, leading to extremely laggy games.

• Players would enter awful messages as the name of their lobby, leading to an excessive amount of hate-speech in the server browser.

• Games had to be designed so you could hop in at any moment which severely limited the creativity of the designers.

So in response, many games adopted a different system of matchmaking. Players, rather than choosing a lobby to join, would sign up to play a certain game mode. The game would search for other similar players, and put them all in a single game.

This allowed players to be matched with others of similar skill - assuming there were enough active players. The game would keep track of each players matchmaking rating (MMR for short). You could track your progress by watching your MMR overtime, or look at the leaderboards to see who was the best in the world.

These days, basically every game uses a system like this. Even for players who choose not to play "ranked" (a game mode where the game shows your rating and encourages competition), the game still tracks their MMR so that matches can be as fair as possible. It's a genius system that has drastically improved the quality of online video games.

ELO

So we know that the game tries to match players of similar skill, but how does it know how skilled each player is? This is where the ELO system comes in.

It was invented back in the 1950s by the a physics professor and chess player named Arpad Elo, who was commissioned by the United States Chess Federation (USCF) to devise a system to rank players accurately. The USCF had previously been using a model called the Harkness system, which was reasonably fair, but sometimes led to ratings which most observers considered inaccurate (source). Elo's new system was based on statistics and probability, and has been the cornerstone of most rating systems since.

Note: For the rest of the blog, MMR and ELO are used interchangeably - they both refer to how skilled the game thinks a player is. ELO is simply the most common example of a MMR.

The basic idea behind the system is that on a given day, a competitor's performance follows a normal distribution centered at the players skill rating. A player's chance to win a given match is determined by probability that a random value generated from their distribution is higher than that of the opponent's.

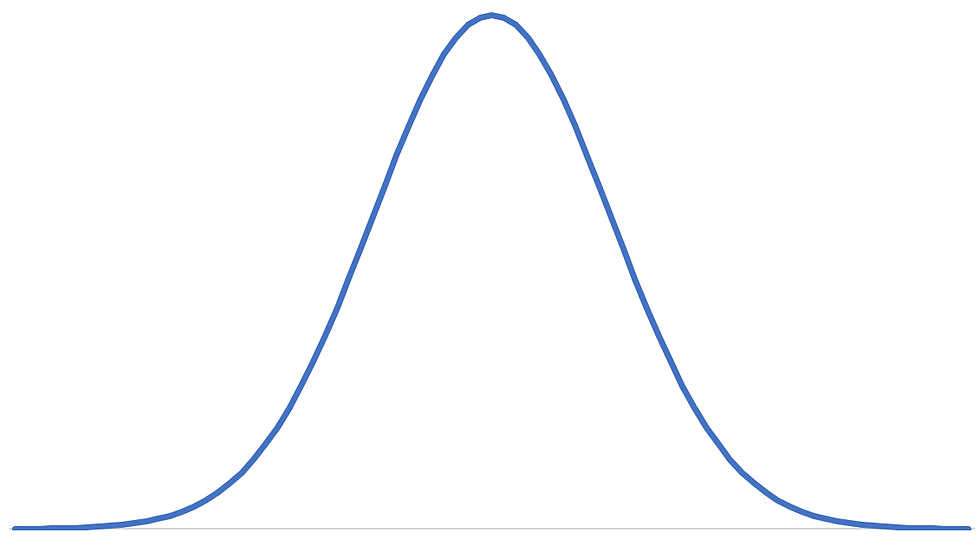
The shape of a normal distribution

After a match is complete, the winning player takes ELO from the losing player, based on how likely they were to win.

Unfortunately, before I can give an example, there are two few parameters in the ELO system.

• Starting ELO: What skill rating does the game give the players at the beginning. I'll use 1000 for this.

• Max ELO gained: What is the maximum ELO a player can gain from a match? I'll say 100 for this example.

• ELO Standard Deviation: How spread out should the ELOs be? I'll use 100 for this example.

• Skill ratings for the players: Players have an actual skill rating that determines how likely they are to win. This isn't actually known of course, but it's what the ELO system is trying to accurately calculate. I'll say that player's skills are distributed randomly around 500.

• Standard distribution of skill per match: How varied is a player's performance in comparison to their skill rating? I'll say that a player's performance has a standard deviation of 75 around their skill rating.

Now, it's very important to understand that the last 2 parameters described are not present in a real-matchmaking system. A player's "skill" and their "distribution" aren't numbers we have access to in real life. These numbers are just there so the simulation can determine a winner and a loser. In video games, the winner and loser and determined, by you know, playing the actual game.

Example

So for example, let's say Bob has an ELO of 1000, and Carol has an ELO of 1100. Since Bob's ELO is lower, he's the underdog in the match. Let's say he upsets Carol and takes home the victory.

We would calculate the ELO gained and lost by asking "How likely was it for Bob's normal distribution to generate a value above Carol's?" Or in other words, how likely was it that Bob would win this match given our current assessment of these two players (their current ELOs).

In this case, using the normal distribution, it was only about 15%. We subtract that value from 100% to get 85%, and give that percentage of the "Max ELO Gained" from earlier to Bob. 100 ELO * 85% = 85 ELO points. We subtract the same from Carol's ELO.

Thus, Bob's new ELO is 1000 + 85 = 1085 and Carol's is 1100 - 85 = 1015.

If you're curious where that 15% came from - we first calculate how many standard deviations above Carol is above Bob - in this case,

1100 ELO - 1000 ELO = 100 ELO = 1 standard deviation

We then see how much of the normal distribution is greater than 1 standard deviation away from the mean to get 15 percent.

Notice how because we thought Bob was unlikely to win the match, he got lots of points. If Carol had won, she only would have been awarded 15 since she was the heavy favorite.

The simulation

To code this up, I went into Unity and spent a few hours creating a graphing system so I could watch the players over time. Here is the result:

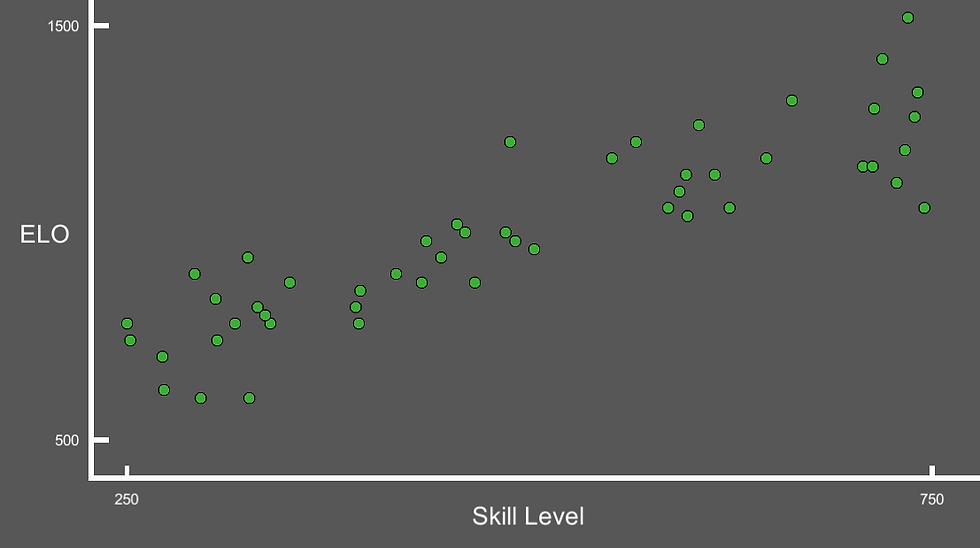
Each player is represented by a dot. The X axis corresponds to a player's Skill Level, or how good at the game they are. The Y axis represents how skilled the game thinks the player is, or their ELO.

Once again, I want to stress that the "skill level" here isn't something a real matchmaking system knows. The only thing the "skill level" of a player is used for is to calculate the winner and loser of a match.

The first step is to generate the players. Their ELOs all start at 1000, as the game has no idea how good they are initially, and their skill levels are distributed evenly around 500.

The resultant graph looks like this. Make sure that it makes sense why the graph looks this way, otherwise you'll be lost trying to understand what is coming.

As expected, the players are placed evenly along the center line at ELO = 1000. The next step is to start simulating some games.

To make things simple, I'll start by saying that when a player wins a game, they gain 10 ELO, and when they lose, they lose 10 ELO. I won't worry about their probability to win or anything like that. I'll show the simulation over the course of 100 games for each player.

As you can see, the rating does accurately give the lower-skill players a low ELO and the better players a high ELO. However, the highly skilled players are soon off the charts, and the bad players are plummeting down towards zero.

This happens because this system doesn't take into skill into account. If a player loses a match in which they are heavily outclassed, it shouldn't hurt their ELO as much as losing a match to someone around their skill level. Similarly, a good player shouldn't gain so much ELO for beating up on the new players.

To fix this, I'll give points based on the system's best guess for who will win. If two similarly ranked players play, the ELO change will be about 50. But if an expert plays against a low-ranked player and wins, they will receive far fewer points (and the loser won't lose much ELO).

Here is the simulation over about 50 games.

As you can see, this system works much better. After not too many games, players' ELOs are fairly stable, indicating that the system has accurately judged their skill. Remember, a players' "skill level" and ELO don't have to be correlated 1:1. The ELO is just a metric for ranking the player based on their performance. In this case, it seems like the best players peak around 1200 ELO.

Note that the actual range of the numbers isn't important - the best chess players have ELOs around 2800. They are simply using a different scale than this simulation, or starting their new players at a higher rating. What's important is a given players ELO in relation to the rest of the player base.

Divisions

While many multiplayer games use this system to keep track of their users, they often will hide the MMR of players. Instead of showing a player their rating, the game gives a "division" to the player that roughly describes the caliber of player they are.

For example, League of Legends has the tiers such as Bronze, Gold and Diamond. This abstraction has been shown to feel more rewarding to the player, as entering a new division feels a lot better to the player than "finally getting 1200 MMR" for example. It also avoids players complaining about "only gaining X" MMR after a game.

The divisions are directly correlated to the MMR of the player. For example, I could divide my ELO system like so:

• Bronze: Below 700

• Silver: 700-850

• Gold: 851-1051

• Diamond: 1051-1251

• Master: 1251 and higher

To show this, I'll color the players in the simulation based on their tier from above. Master will be purple.

Once again, this is purely for the pleasure and experience of the player. The developers of a game can tweak the ranges of different tiers to give them varying levels of exclusivity. For example, the "master" rank in League of Legends comprises less than a half percent of the total player base.

An individual

This is a great system for organizing an established player base in accordance with their skill, but how is the experience for a new player?

I'll add a new player (shown in red) to an existing ELO distribution. Over the games that they play, I will slowly increase their skill as they become more experienced at the game. You'll be able to see the slow and gradual "climb" that enthralls many competitive online players around the globe.

Of course there's a lot more that could be added to this simulation. For example, the players are currently playing matches versus other random players. A more accurate system would match the players against opponents of a similar ELO. This wouldn't change much, though, as players would still eventually end up at their correct rank. Overall, I think this simulation did a pretty good job simulating a matchmaking system.

Hopefully this gives you some insight into how online matchmaking systems rank players. Catch you in the next one!